[그래프 탐색] 깊이 우선 탐색[DFS]와 너비 우선 탐색[BFS] 알고리즘
탐색 : 주어진 많은 양의 데이터에서 자신이 원하는 데이터를 찾아내는 알고리즘을 의미한다. 주어진 데이터의 유형에 따라 적절한 탐색 알고리즘을 사용하는 것이 중요하며, 탐색의 대표적인 알고리즘으로 DFS와 BFS가 있다. 그런데 DFS와 BFS를 제대로 이해하려면 기본 자료구조인 스택과 큐에 대한 이해가 필요하며 재귀함수 역시 사용하므로 선행학습이 필요하다.
[자료구조] 스택(Stack)과 큐(Queue)
● 스택[Stack] : 끝에서만 자료를 넣고 뺄 수 있는 선형 자료구조 스택이란 프링글스의 과자를 위에서부터 꺼내 먹는 것처럼 삽입과 삭제 연산이 후입선출(LIFO)로 이뤄지는 자료구조를 말합니다.
sjm2449.tistory.com
DFS와 BFS의 근본
근본적인 것은 처음부터 끝까지 모든 노드들을 다 방문하여 뒤지겠다.
특히 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야 한다.
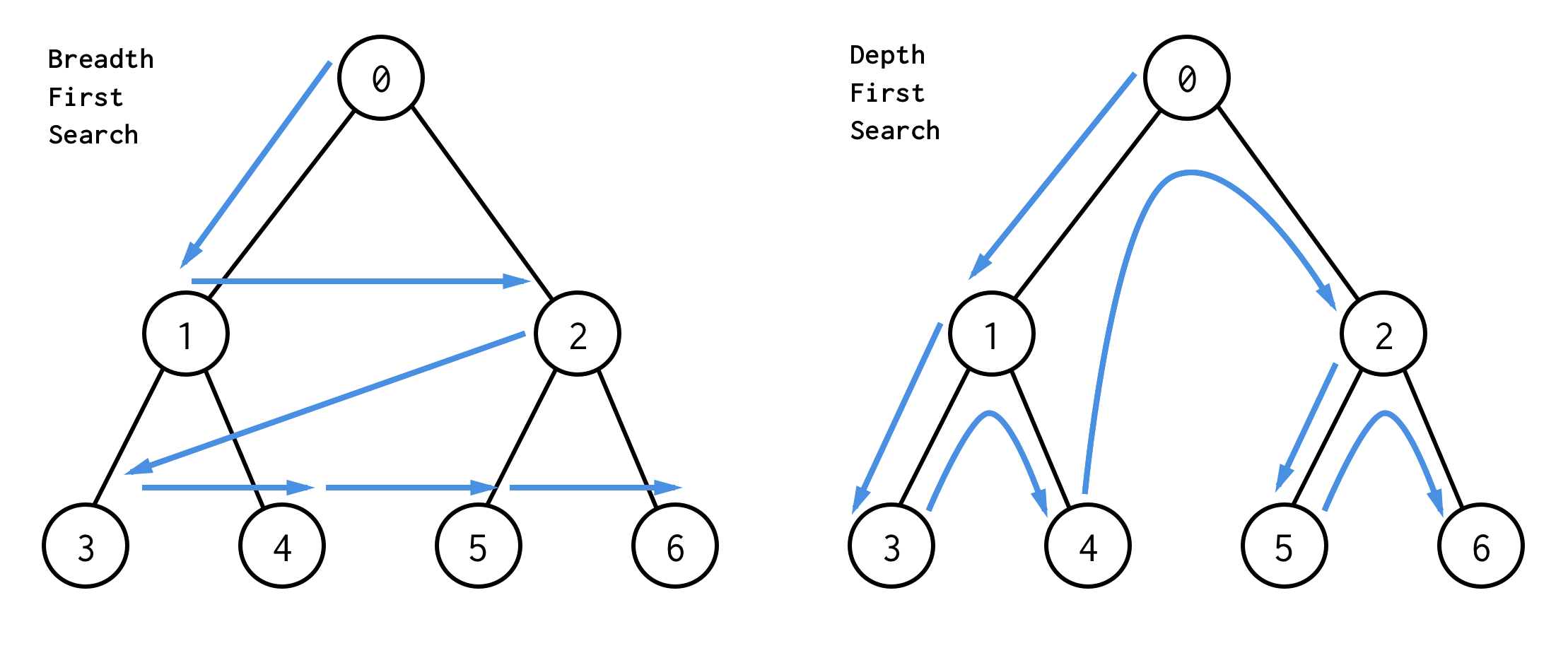
● 깊이 우선 탐색[DFS] : 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색
DFS란 그래프의 시작 노드에서 출발하여 탐색할 한 쪽 지점을 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘 입니다
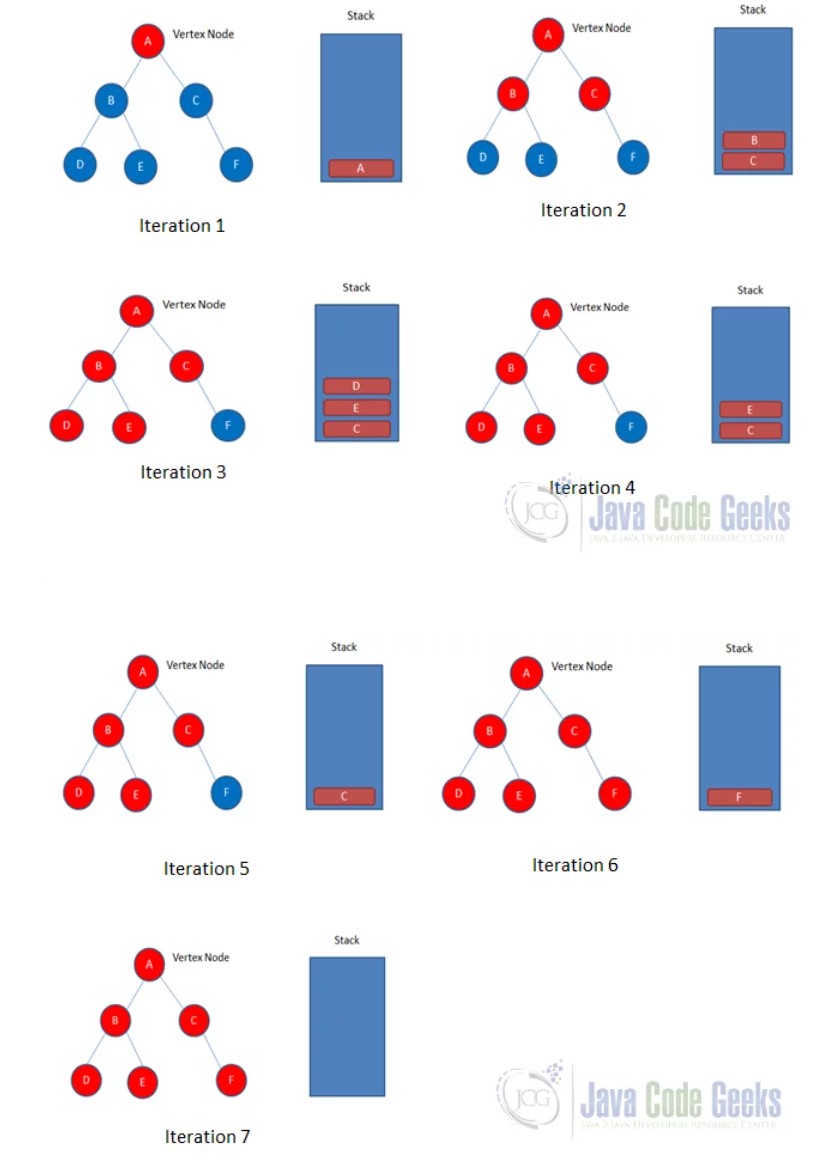
1. DFS의 특징
1. 스택 성질을 갖는 재귀함수를 이용하므로 스택 오버플로에 유의해야 한다.
2. 시간 복잡도의 경우 O(V+E)이다. (데이터의 개수가 N인 경우 O(N)의 시간 소요)
3. BFS보다 간단하게 작성할수 있으나, BFS보다 속도가 느리다
※ 스택 오버플로 : 수용할 수 있는 데이터의 크기를 이미 가득 찬 상태에서 삽입연산을 수행할때 발생
2. DFS의 풀이 과정 [맨 뒤부터 처리]
1. DFS를 시작할 노드를 정한 후 시작 노드를 스택에 삽입하고 방문 처리를 한다.
2. 스택의 최상단 노드를 꺼낸후 꺼낸 노드의 인접노드를 다시 스택에 넣고 방문 처리한다.
- 방문하지 않은 인접노드가 없으면 스택에서 최상단 노드를 꺼낸다.
3. 스택 자료구조에 값이 없을 때까지 반복한다.
1번 출발 ----> 2, 3, 4 [2, 3, 4]
4번 갈래 ----> 8, 9 [2,3,8,9]
9번 갈래 ----> 없어 [2,3,8]
8번갈래 ----> 11, 12 [2,3,11,12]
12번갈래 ----> 없어 [2,3,11]
11번갈래 ----> 없어 [2,3]
3번갈래 ----> 없어 [2]
2번갈래 ----> 없어 []
3. DFS 구현
graph = [ [], [2,3], [1], [1,4,5], [3,5], [3,4] ]
visited = [False] * len(graph) # 방문처리(전부 방문 x)
def DFS (graph, v, visited):
visited[v] = True # 각 노드 방문 처리
for i in graph[v]:
if not visited[i]: # 방문 여부 확인 (False -> 노드 확인)
dfs(graph, i, visited)
DFS(graph, 1, visited)● 넓이 우선 탐색[BFS] : 가까운 노드부터 완벽하게 탐색하고 넘어가는 탐색
BFS란 시작 노드에서 출발해 시작 노드를 기준으로 가까운 노드를 전부 방문하면서 탐색하는 알고리즘이다. BFS의 구현에서는 선입선출의 방식으로 탐색하므로 큐 자료구조를 이용하는 것이 정석이며, 특히 deque를 사용한다.
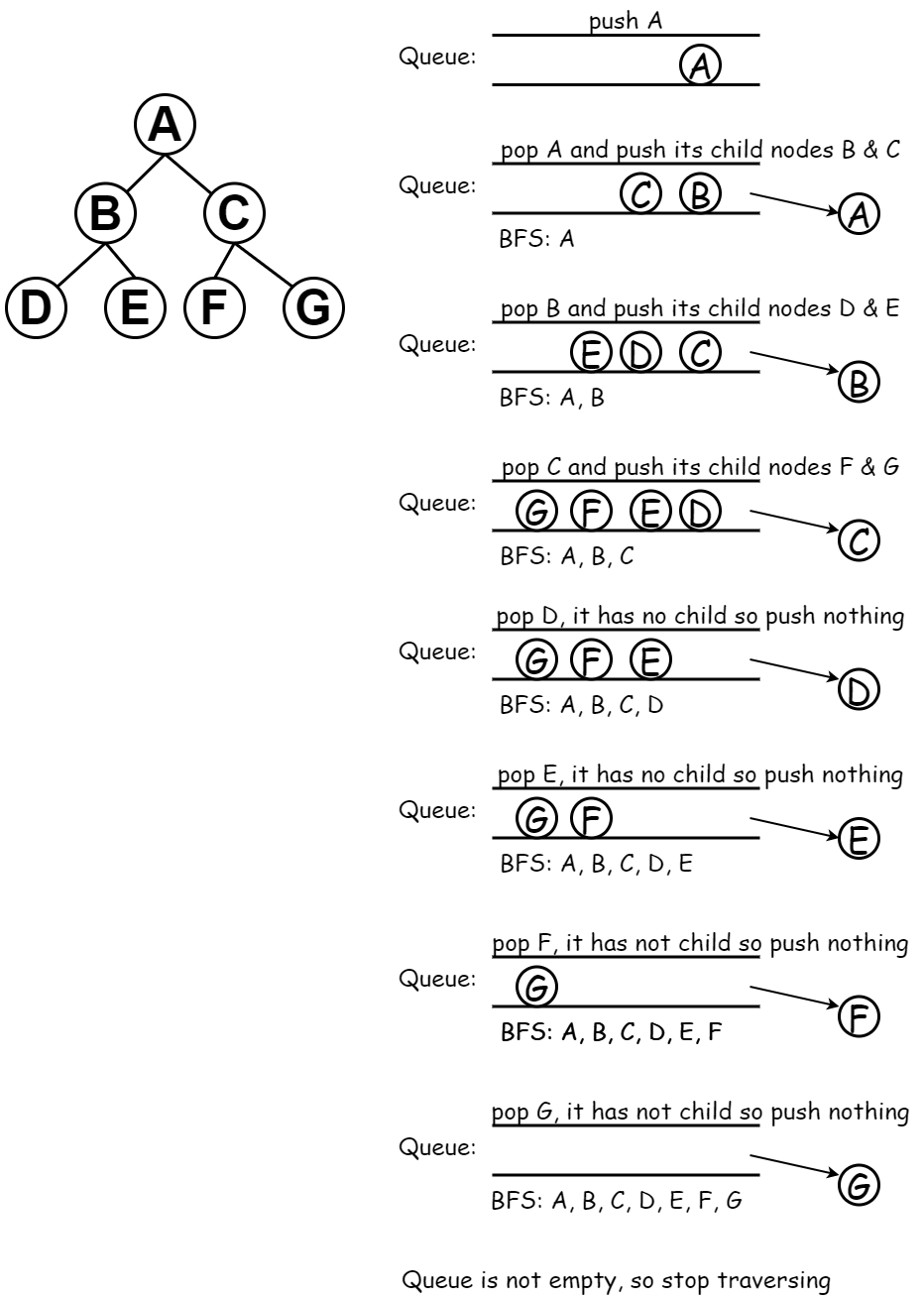
1. BFS의 특징
1. 큐 성질을 갖는 자료함수를 이용하고 실제로 deque 라이브러리를 사용하여 구현이 간단하다.
2. 시간 복잡도의 경우 deque를 사용하는 경우 O(N)이며, 실제 수행시간은 DFS보다 좋은 편이다.
2. BFS의 풀이 과정 [맨 앞에서 부터 처리]
1. BFS를 시작할 노드를 정한 후 시작 노드를 큐에 삽입하고 방문 처리를 한다.
2. 큐에서 노드를 꺼낸 후 해당 노드의 인접 노드 중에서 방문하지 않는 노드를 모두 큐에 삽입하고 방문 처리를 한다.
3. 큐 자료구조에 값이 없을 때까지 반복한다.
1번갈래 ----> 3, 4, 5 [3, 4, 5]
3번갈래 ----> 6,7 [4,5,6,7]
4번갈래 ----> 8 [5,6,7,8]
5번갈래 ----> 없어 [6,7,8]
6번갈래 ----> 없어 [7,8]
7번갈래 ----> 없어 [8]
8번갈래 ----> 없어 []3. DFS 구현
from collections import deque
graph = [[], [2,3], [1], [1,4,5], [3,5], [3,4]]
visited = [False] * len(graph)
def BFS (graph, start, visited):
queue = deque([start])
visited[start] = True
while queue:
v = queue.popleft()
for i in graph[v]:
if not visited[i]:
queue.append(i)
visited[i] = True
BFS(graph, 1, visited)deque에 대한 이해가 필요
참고서적
Do it! 알고리즘 코딩 테스트: 파이썬 편 (코딩 테스트를 처음 준비하는 취준생의 필독서!)