[정렬] 빠른 정렬 (병합, 퀵) 알고리즘

● 병합[Merge] 정렬 : 데이터를 분활하고 분활한 집합을 정렬하여 합침

병합정렬의 경우 배열을 앞과 뒤로 나눠서 각각 최소 단위(1)까지 분활하고 분활한 집합을 정렬하며 합치는 알고리즘이다.

https://levelup.gitconnected.com/visualizing-designing-and-analyzing-the-merge-sort-algorithm-cf17e3f0371f

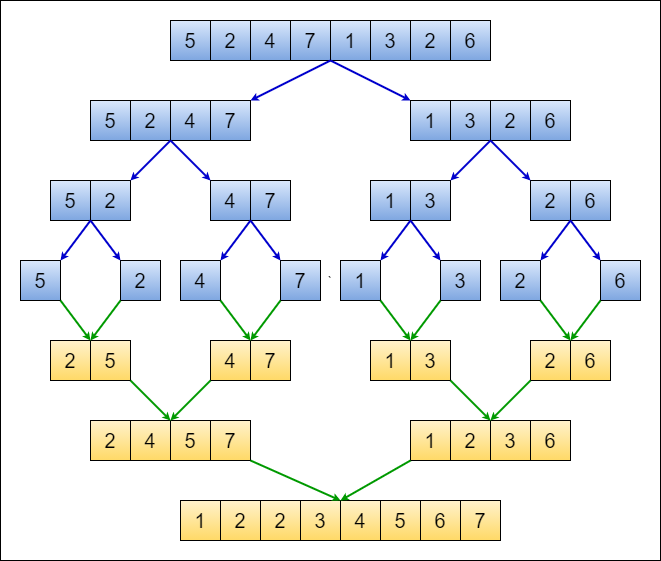
1. 병합 정렬의 특징

1. 병합 정렬의 시간 복잡도는 O(nlogn)으로

2. 병합 정렬은 n개의 개체가 있다면 O(n)만큼의 추가 공간이 필요

 

2. 병합 정렬 과정

1. Divide [O(1)] : n개의 값을 1개가 남을때까지 두 개의 n/2 keys로 계속 나눈다.

2. Merge [2T(n/2)] : 합병정렬을 사용하여 두 개의 배열을 정렬한다.

3. Combine [O(n)] : 두 개의 정렬된 배열을 원래 하나의 배열로 만든다.

     - 병합의 과정에서 투 포인터의 개념을 사용하며 반드시 숙지 할 것!!!!

 

3. 병합 정렬 구현

listA = [1,41,32,31,42,32,10]

def mergeSort(listA) :
  if len(listA) <= 1:
    return listA
  mid = len(listA)//2
  left = mergeSort(listA[:mid]) # 재귀 함수
  right = mergeSort(listA[mid:]) # 재귀 함수
  return merge(left,right)

def merge(left, right):
  merged = []
  while (len(left)>0) or (len(right)>0):
    if len(right) <= 0: # 왼쪽에만 아이템이 있으면
      return merged + left
    elif len(left) <= 0: # 오른쪽에만 아이템이 있으면
      return merged + right
    else: # 왼쪽과 오른쪽에 모두 있으면
      if left[0] <= right[0]:
        merged.append(left[0])
        del left[0] 
      else :
        merged.append(right[0])
        del right[0]
  return merged

print(mergeSort(listA))
>>> [1, 10, 31, 32, 32, 41, 42]

※ 정렬된 두 개의 배열이 주어진 문제에서 병합

import heapq
a = [2,4,6,8,10]
b = [1,3,5,7,9]
c = list(heapq.merge(a, b))
print(c)
>>> [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

---

● 퀵[Quick] 정렬 : Pivot을 설정하여 크기 별로 리스트를 반으로 나누는 정렬

Pivot을 설정한 다음 큰 수와 작은 수를 교환한 후 리스트를 반으로 나누는 방식의 정렬

https://www.w3resource.com/csharp-exercises/searching-and-sorting-algorithm/searching-and-sorting-algorithm-exercise-9.php

 

1. 퀵 정렬의 특징

1. 퀵의 시간복잡도

   - 무작위 배열(평균적인 상황) : O(nlogn)

   - 정렬된 배열(최악의 상황) : O(n^2)

2. 일반적으로 사용되는 아주 빠른 정렬 알고리즘이다.

 

2. 퀵 정렬 과정

1. 데이터를 분활하는 pivot을 설정한다. (대표적인 분활 방식 호어 분활 방식 기준)

   - 호어 분활 방식 : 리스트에서 첫 번째 데이터를 피벗으로 설정

2. pivot을 기준으로 다음 a~e 과정을 거쳐 데이터를 2개로 분활한다.

   2-a. start 지점의 데이터가 pivot보다 작은 경우 start 지점을 오른쪽으로 한칸 이동한다.

   2-b. end 지점의 데이터가 pivot보다 큰 경우 end 지점을 왼쪽으로 한칸 이동한다.

   2-c. start의 데이터가 pivot보다 크고, end의 데이터가 pivot보다 작은 경우 start와 end의 데이터를 서로 swap하고

          start는 오른쪽으로 한칸 end는 왼쪽으로 한칸 이동한다.

   2-d. start > end가 될 때까지 위의 과정을 반복한다.

   2-e. start > end가 되면 작은 데이터와 pivot을 교체한다.

3. 분리 집합에서 다시 pivot을 선정하여 분리집합이 1개가 될 때까지 반복한다.

 

3. 퀵 정렬 과정

3.1. 기본정렬

list = [5, 7, 9, 0, 3, 1, 6, 2]

def QuickSort (list, start, end):
  if start >= end:
    return
  pivot = start
  left = start+1
  right = end
  while left <= right:
    while left <= end and list[left] <= list[pivot]: # 왼쪽 값이 피벗보다 작으면 오른쪽으로 +1
      left += 1
    while right > start and list[right] >= list[pivot]: # 오른쪽 값이 피벗보다 크면 왼쪽으로 -1
      right -= 1
    if left > right : # 엇갈렸다면 작은 데이터와 피벗을 교체
      list[pivot], list[right] = list[right], list[pivot]
    else : # 엇갈리지 않았다면 작은 데이터와 큰 데이터 교체
      list[left], list[right] = list[right], list[left]
    QuickSort(list, start, right -1)
    QuickSort(list, right + 1, end)
  
QuickSort(list, 0, len(list)-1)
print(list)
>>> [0, 1, 2, 3, 5, 6, 7, 9]

3.2. 파이썬의 장점을 살린 퀵 정렬

list = [5, 7, 9, 0, 3, 1, 6, 2]

def QuickSort(list):
  if len(list) <= 1:
    return list
  
  pivot = list[0]
  tail = list[1:]

  left = [i for i in tail if i <= pivot]
  right = [i for i in tail if i > pivot]

  return QuickSort(left) + [pivot] + QuickSort(right)

print(QuickSort(list))

---

참고서적

Do it! 알고리즘 코딩 테스트: 파이썬 편 (코딩 테스트를 처음 준비하는 취준생의 필독서!)

이것이 취업을 위한 코딩 테스트다 with 파이썬 (취업과 이직을 결정하는 알고리즘 인터뷰 완벽 가이드)

Do it! 자료구조와 함께 배우는 알고리즘 입문: 파이썬 편 (내 손으로 직접 코딩하며 확인한다)